Théories sur la programmation image
Théorie sur la 2D
repere 2D:
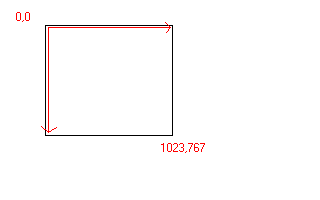 Un écran est un repere 2D. Le repere est orienté comme sur le schéma.
Ainsi, chaque pixel est représenté par une coordonnée x,y. La
résolution de votre écran (ou de votre fenetre) défini le nombre de
pixels. Par exemple 1024*768 pixels, etc...
x varie dans ce cas entre 0 et 1023, y entre 0 et 767. Le point en
bas a droite aura pour coordonnée 1023,767.
Un ensemble rectangulaire de pixels est appelé un bitmap.
Ainsi l'écran est un bitmap.
Un écran est un repere 2D. Le repere est orienté comme sur le schéma.
Ainsi, chaque pixel est représenté par une coordonnée x,y. La
résolution de votre écran (ou de votre fenetre) défini le nombre de
pixels. Par exemple 1024*768 pixels, etc...
x varie dans ce cas entre 0 et 1023, y entre 0 et 767. Le point en
bas a droite aura pour coordonnée 1023,767.
Un ensemble rectangulaire de pixels est appelé un bitmap.
Ainsi l'écran est un bitmap.
couleurs :
 Toute couleur sur ordi est définie par 3 composantes : rouge, vert,
bleu. En dosant les intensités de ces 3 couleurs, on reforme TOUTES
les couleurs. Par exemple : le noir est 0% de rouge, 0% de vert, 0%
de bleu. Le blanc, c'est 100% des 3. Le violet, c'est 100% de rouge,
100% de bleu, 0% de vert...
Toute couleur sur ordi est définie par 3 composantes : rouge, vert,
bleu. En dosant les intensités de ces 3 couleurs, on reforme TOUTES
les couleurs. Par exemple : le noir est 0% de rouge, 0% de vert, 0%
de bleu. Le blanc, c'est 100% des 3. Le violet, c'est 100% de rouge,
100% de bleu, 0% de vert...
profondeur de pixel :
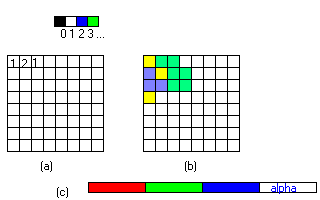 A chaque pixel est associé une couleur. C'est uniquement ainsi qu'on
défini une image.
Il existe plusieurs formats pour coder une couleur.
- mode indexé 16 couleurs (a) : chaque pixel coute 4 bits (1/2
octet). 1/2 octet stocke 16 possibilités, donc dans cette résolution,
on ne pourra avoir que 16 couleur affichables. On défini pour chaque
pixel du bitmap un nombre entre 0 et 15. Ailleurs en mémoire, il
existe ce qu'on appelle une palette. C'est cette palette qui dit "la
couleur 0 est du noir, la couleur 1 est du blanc, la couleur 2 est du
bleu, etc...". L'avantage de cette méthode est que si on change la
palette (on dit que le 2 est maintenant du rouge), alors tous les
pixels bleus de l'écran deviennent automatiquement rouge.
A chaque pixel est associé une couleur. C'est uniquement ainsi qu'on
défini une image.
Il existe plusieurs formats pour coder une couleur.
- mode indexé 16 couleurs (a) : chaque pixel coute 4 bits (1/2
octet). 1/2 octet stocke 16 possibilités, donc dans cette résolution,
on ne pourra avoir que 16 couleur affichables. On défini pour chaque
pixel du bitmap un nombre entre 0 et 15. Ailleurs en mémoire, il
existe ce qu'on appelle une palette. C'est cette palette qui dit "la
couleur 0 est du noir, la couleur 1 est du blanc, la couleur 2 est du
bleu, etc...". L'avantage de cette méthode est que si on change la
palette (on dit que le 2 est maintenant du rouge), alors tous les
pixels bleus de l'écran deviennent automatiquement rouge.
- mode indexé 256 couleurs : la meme chose, mais 1 octet par pixels,
et donc une palette de 256 nuances.
- mode couleur vraie 16 bits(b): Chaque pixel est indépendant, il
coute 2 octets. On y met : 5 bits pour le rouge, 6 bits pour le vert,
5 bits pour le bleu. On met 1 bit de plus pour le vert car l'oeil
humain est plus sensible aux différences de vert. Cela laisse 32
nuances de rouge et de bleu, 64 nuances de vert. Ce mode est
completement dépassé car pas pratique.
- mode couleur vraie 24 bits: le plus intuitif : chaque pixel
consomme 3 octets, 1 pour chaque composante RGB. Donc 256 nuances de
chaque couleur, ce qui est largement suffisant pour faire des
dégradés optimals.
- mode couleur vraie 32 bits (c): (4 octets par pixels) Afin
d'accélérer les transferts, on préfere prendre les octets 4 par 4,
plutot que 3 par 3 (pas pratique). On rajoute donc un 4e octet par
pixel. Pas question d'augmenter les R,G,B, stockés chacun sur 1 octet
pour 2 raisons : d'abord, l'oeil humain ne verrait pas la différence,
ensuite, ce serait de nouveau le bordel niveau mémoire, il faudrait
rentrer au niveau binaire au lieu de rester a manipuler des octets.
Donc le 4e octet a été appelé ALPHA. Il s'agit d'un coefficient de
transparence, utilisé dans pas mal de moteurs : si alpha=255 : le
pixel est opaque, si alpha=0, il est invisible, s'il est entre, alors
il est plus ou moins transparent.
Blitting :
 Toute la 2D repose sur le blitting. L'écran est un bitmap. On colle
par exemple un bitmap de la taille de l'écran dessus, qui fera le
fond, puis on charge d'autres petits bitmaps rectangulaires, et on
coupe et colle les images sur le bitmap de l'écran, du collage en
somme !
On appelle cette opération "blit".
Cependant, si on s'arrete la, alors on voit nettement que l'on colle
des rectangles (a).
On défini une "keycolor", c'est a dire une couleur qui sera invisible
pour chaque bitmap. Ainsi, lorsqu'un bitmap est collé, la couleur
invisible n'apparait pas, ce qui rend la chose plus réaliste (b)
Toute la 2D repose sur le blitting. L'écran est un bitmap. On colle
par exemple un bitmap de la taille de l'écran dessus, qui fera le
fond, puis on charge d'autres petits bitmaps rectangulaires, et on
coupe et colle les images sur le bitmap de l'écran, du collage en
somme !
On appelle cette opération "blit".
Cependant, si on s'arrete la, alors on voit nettement que l'on colle
des rectangles (a).
On défini une "keycolor", c'est a dire une couleur qui sera invisible
pour chaque bitmap. Ainsi, lorsqu'un bitmap est collé, la couleur
invisible n'apparait pas, ce qui rend la chose plus réaliste (b)
Le principe donc de la 2D est de charger des images (a partir d'un
fichier BMP par exemple, et de les coller au bon endroit).
Double Buffering :
 Nous voulons faire une animation. Pour cela, il faut, pour chaque
image, coller le personnage un peu plus loin que l'image d'avant.
Pour cela, il faut d'abord effacer l'image actuelle, puis la recréer
en mettant le perso plus loin. L'ordinateur a beau etre rapide
(plusieurs milliers voir centaines de milliers de blit par seconde),
si on fait cela, on verra notre personnage clignoter : car pendant
une fraction de seconde, entre le temps ou c'est effacé, et le temps
ou le personnage est redessiné plus loin, il n'y a plus le personnage
: donc il apparait et disparait tres vite --> clignotement.
Pour palier ce probleme, on défini 2 bitmap d'écrans. L'un est
visible a l'écran. Pendant ce temps, on prépare, sur le 2e, invisible
a l'écran, la nouvelle image. Une fois fini, on "flip", c'est a dire
qu'on dit que maintenant, c'est la 2e image qui est affichée, et la
1ere image que l'on va pouvoir modifier. La 2e image, toute prete
remplace la 1ere : comme au cinéma, on n'a plus de clignotement.
A la différence du cinéma qui stocke toutes ses images, ici, l'ordi
calcule sans arret l'image suivante, et l'affiche qu'une fois
terminée, afin de calculer la suivante de nouveau...
Nous voulons faire une animation. Pour cela, il faut, pour chaque
image, coller le personnage un peu plus loin que l'image d'avant.
Pour cela, il faut d'abord effacer l'image actuelle, puis la recréer
en mettant le perso plus loin. L'ordinateur a beau etre rapide
(plusieurs milliers voir centaines de milliers de blit par seconde),
si on fait cela, on verra notre personnage clignoter : car pendant
une fraction de seconde, entre le temps ou c'est effacé, et le temps
ou le personnage est redessiné plus loin, il n'y a plus le personnage
: donc il apparait et disparait tres vite --> clignotement.
Pour palier ce probleme, on défini 2 bitmap d'écrans. L'un est
visible a l'écran. Pendant ce temps, on prépare, sur le 2e, invisible
a l'écran, la nouvelle image. Une fois fini, on "flip", c'est a dire
qu'on dit que maintenant, c'est la 2e image qui est affichée, et la
1ere image que l'on va pouvoir modifier. La 2e image, toute prete
remplace la 1ere : comme au cinéma, on n'a plus de clignotement.
A la différence du cinéma qui stocke toutes ses images, ici, l'ordi
calcule sans arret l'image suivante, et l'affiche qu'une fois
terminée, afin de calculer la suivante de nouveau...
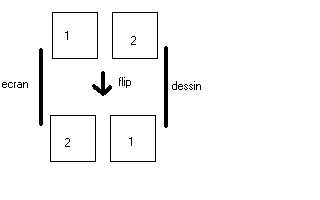
Si on regarde l'image : en haut, l'image 1 est a l'écran, on dessine la
suite sur l'image 2. Puis on flip, ainsi c'est l'image 2 qui est vers l'écran
et l'image 1 prete a etre modifiée. Si on reflip, on se retrouve de nouveau dans
la situation du haut.
Clipping :
 lorsqu'un personnage est sur le bord de l'écran, il faut qu'on ne le
voie qu'a moitié. Pour cela, il ne faut donc pas l'afficher
completement, mais juste la partie visible, il faut donc une phase de
prédécoupage, ou l'ordi selectionne juste la partie a afficher. C'est
un "clipping". Tous les moteurs actuels gerent le clipping
automatiquement : si vous blittez en personnage sur l'écran, sur le
bord, ou meme dehors, ils gerent ça tout seul. Les cartes graphiques
sont meme en partie faites pour cela.
lorsqu'un personnage est sur le bord de l'écran, il faut qu'on ne le
voie qu'a moitié. Pour cela, il ne faut donc pas l'afficher
completement, mais juste la partie visible, il faut donc une phase de
prédécoupage, ou l'ordi selectionne juste la partie a afficher. C'est
un "clipping". Tous les moteurs actuels gerent le clipping
automatiquement : si vous blittez en personnage sur l'écran, sur le
bord, ou meme dehors, ils gerent ça tout seul. Les cartes graphiques
sont meme en partie faites pour cela.
RAM OU VRAM :
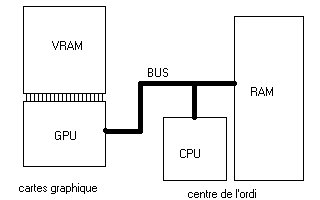 L'ordinateur contient plusieurs mémoires : une centrale, appelée RAM,
et une sur la carte graphique, appelée VRAM. Si on garde toutes les
images en RAM, alors, a chaque nouvelle frame (nouvelle image
calculée), (donc 50 par secondes par exemple si on veut une animation
fluide), toute l'image est evoyée sur le bus. A titre indicatif, une
image de 1024*768, 32bits, fait a peu pres 4Mo. Si on doit en envoyer
50 par seconde, cela fait une taux de circulation de 50*4 = 200 Mo
sur le bus, rien que pour la vidéo. C'est énorme : beaucoup d'ordis
rament. Je précise que certains joueurs trouvent que 50 images par secondes,
c'est lent, et veulent avoisiner les 100 fps (frame per second = images par secondes)
L'ordinateur contient plusieurs mémoires : une centrale, appelée RAM,
et une sur la carte graphique, appelée VRAM. Si on garde toutes les
images en RAM, alors, a chaque nouvelle frame (nouvelle image
calculée), (donc 50 par secondes par exemple si on veut une animation
fluide), toute l'image est evoyée sur le bus. A titre indicatif, une
image de 1024*768, 32bits, fait a peu pres 4Mo. Si on doit en envoyer
50 par seconde, cela fait une taux de circulation de 50*4 = 200 Mo
sur le bus, rien que pour la vidéo. C'est énorme : beaucoup d'ordis
rament. Je précise que certains joueurs trouvent que 50 images par secondes,
c'est lent, et veulent avoisiner les 100 fps (frame per second = images par secondes)
Il est donc conseillé de garder les images en VRAM, c'est une mémoire
dans la carte graphique, optimisée pour ce genre de transferts, en
parallele. Les gains de vitesse sont considérables.
Les 2 bufferes du double buffer sont donc gardés en VRAM. Il est
conseillé de garder le maximum d'autres bitmaps (personnages) en VRAM
également. S'il n'y a pas assez de mémoire, c'est au programmeur de
juger lesquels garder en VRAM.
extra legend :
CPU = Central processor unit : processeur central, c'est
lui qui gere les calculs centraux.
GPU = Graphic processor unit : processeur sur la carte graphique
lui est spécialisé dans l'affichage et le traitement 2D/3D, il décharge
le CPU de pas mal de taches graphiques.
Théorie sur la 3D temps réel
Ici, je vais parler des théories sur les moteurs 3D bas niveau connus. Je prendrai comme exemple OpenGL : je mettrai rapidement la commande qui permet d'obtenir l'effet du paragraphe.
Repere 3D :
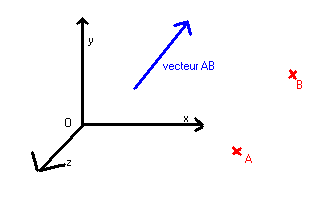 Le repere 3D est un repere dans l'espace : l'origine est le point O, et la base est x,y,z.
Ainsi, dans l'espace, on représente un point par 3 coordonnées.
Le repere 3D est un repere dans l'espace : l'origine est le point O, et la base est x,y,z.
Ainsi, dans l'espace, on représente un point par 3 coordonnées.
On peut également manipuler des vecteurs pour divers algorithmes que l'on verra plus tard.
Dans l'espace 3D (ici appelé Espace Affine), un vecteur n'est jamais que la différence entre 2 points, et se calcule
en faisant la différence de chacune des 3 coordonnées de chaque point.
Contrairement à la 2D, le repere 3D est composé de nombres réels (a virgule), c'est un repere de R3.
Ainsi, un point peut avoir comme coordonnées : 0.5,-0.3513,2
Polygones :
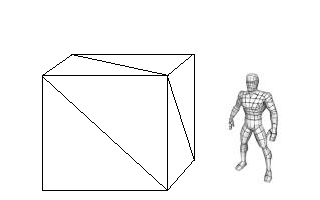 Tous les moteurs 3D temps réels actuels marchent de façon simple : vous donnez des triangles a la carte graphique, et elle les affiche correctement. Un triangle, c'est 3 points, et 3 points, c'est 3 nombres a virgule, donc ça fait 9 nombres a passer par triangle. Nous verrons comment cela marche par la suite.
Tous les moteurs 3D temps réels actuels marchent de façon simple : vous donnez des triangles a la carte graphique, et elle les affiche correctement. Un triangle, c'est 3 points, et 3 points, c'est 3 nombres a virgule, donc ça fait 9 nombres a passer par triangle. Nous verrons comment cela marche par la suite.
Il faut savoir que TOUS LES JEUX 3D actuels sont faits avec des polygones. Ces polygones sont tous décomposés en triangles :
le triangles étant le polygone le plus simple. Ainsi, ce que vous voyez dans votre jeu 3D préféré, c'est uniquement des triangles...
note : certains me diront "on voit aussi des quads", mais je leur réponds que les quads sont faits avec 2 triangles...
Fonctions OpenGL :glBegin(GL_TRIANGLES); glVertex3f(...); ...
Caméra :
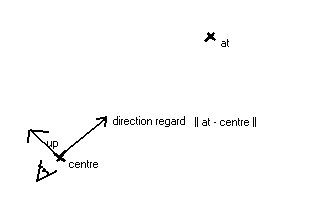 Pour modéliser une scene en 3D, il faut donc donner des triangles dans l'espace. Cependant, il faut également définir une caméra, pour savoir de quel endroit on regarde la scene.
La caméra se défini, par 3 données, disons que la caméra est vos yeux :
Pour modéliser une scene en 3D, il faut donc donner des triangles dans l'espace. Cependant, il faut également définir une caméra, pour savoir de quel endroit on regarde la scene.
La caméra se défini, par 3 données, disons que la caméra est vos yeux :
- le centre (un point de l'espace) : vous etes dans une piece, vous voulez avoir une belle vue, déplacez vous dans la piece jusqu'a l'endroit qui vous convient.
- le "at" : définissez un autre point de l'espace : vous regardez dans cette direction
- le "up" : hochez la tete et comprenez l'utilité du "up", c'est un vecteur, cette fois ci, qui défini le haut : si vous hochez la tete, le haut de votre tete "regarde" ailleurs, cependant, le centre et le at ne bougent pas.
Il est donc essentiel de définir ces parametres pour fixer la caméra sans ambiguité.
Fonctions OpenGL :gluLookat(...);
Frustrum :
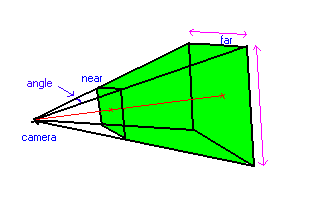 Vous le savez peut etre, mais il existe des caméras grand angle, et des caméras de moins grand angle. Les moteurs 3D permettent de paramétrer toute sorte de parametres, qui définiront le frustrum de vision, c'est a dire que ce que vous verrez est ce qu'il y aura a l'intérieur de cette pyramide coupée verte, et vous ne verrez pas ce qu'il y a à l'extérieur.
On définit le frustrum de la manière suivante (il en existe d'autres manieres mais ça revient au meme)
Vous le savez peut etre, mais il existe des caméras grand angle, et des caméras de moins grand angle. Les moteurs 3D permettent de paramétrer toute sorte de parametres, qui définiront le frustrum de vision, c'est a dire que ce que vous verrez est ce qu'il y aura a l'intérieur de cette pyramide coupée verte, et vous ne verrez pas ce qu'il y a à l'extérieur.
On définit le frustrum de la manière suivante (il en existe d'autres manieres mais ça revient au meme)
- l'angle d'ouverture (angle bleu)
- le rapport entre largueur et hauteur (axes violets) (4/3, 16/9, etc...)
- la distance MIN : distance du plan "near" a la caméra
- la distance MAX : distance du plan "far" a la caméra
Attention !! Si vous définissez MIN trop pres, la machine fait des erreurs d'arrondis, et les rendus 3D sont moches...
Fonctions OpenGL :gluPerspective(...); glFrustrum(...); ...
Rasterisation :
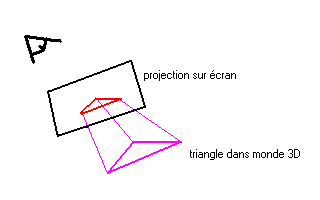 Ce monde en 3D composé de nombres réels, qui se trouve en mémoire, composé de cette soupe de triangles, doit, pour etre rendu, etre projeté sur l'écran 2D (ce sera un dessin 3D sur l'écran). Pour cela, l'ordi garde en mémoire un tableau de 1024*768 pixels par exemple, avec une certaine profondeur de couleur (voir théorie 2D la dessus) Tout comme la 2D, il sera souhaitable de gérer un double buffering, donc avoir 2 tableaux de couleurs que l'on "flip"
La différence, c'est que les images ne seront pas faites a partir de copier coller de vignettes comme dans la 2D, mais d'un monde 3D rasterisé, c'est a dire projeté sur l'écran.
Pour rasteriser, l'ordi effectue l'opération suivante :
pour chaque triangle, il calcule les coordonnée des 3 sommets projetés (voir ce calcul plus loin), en s'appuyant sur les parametres définis de la caméra et de la position des triangles dans l'espace.
Il conserve en outre la distance de chaque sommet a la caméra. Pour que ce soit rapide, il considere la distance au carré, ce qui évite un calcul de racine carrée.
Sachant que la projection d'un triangle est un triangle, il lui suffit de dessiner le triangle a l'écran...
si les projections des sommets sont a l'extérieur de l'écran, il ne rend pas les triangles, ou alors il les clip. (voir clipping dans la 2D)
Ce monde en 3D composé de nombres réels, qui se trouve en mémoire, composé de cette soupe de triangles, doit, pour etre rendu, etre projeté sur l'écran 2D (ce sera un dessin 3D sur l'écran). Pour cela, l'ordi garde en mémoire un tableau de 1024*768 pixels par exemple, avec une certaine profondeur de couleur (voir théorie 2D la dessus) Tout comme la 2D, il sera souhaitable de gérer un double buffering, donc avoir 2 tableaux de couleurs que l'on "flip"
La différence, c'est que les images ne seront pas faites a partir de copier coller de vignettes comme dans la 2D, mais d'un monde 3D rasterisé, c'est a dire projeté sur l'écran.
Pour rasteriser, l'ordi effectue l'opération suivante :
pour chaque triangle, il calcule les coordonnée des 3 sommets projetés (voir ce calcul plus loin), en s'appuyant sur les parametres définis de la caméra et de la position des triangles dans l'espace.
Il conserve en outre la distance de chaque sommet a la caméra. Pour que ce soit rapide, il considere la distance au carré, ce qui évite un calcul de racine carrée.
Sachant que la projection d'un triangle est un triangle, il lui suffit de dessiner le triangle a l'écran...
si les projections des sommets sont a l'extérieur de l'écran, il ne rend pas les triangles, ou alors il les clip. (voir clipping dans la 2D)
Fonctions OpenGL :glSwapbuffers(); ...
Affichage rapide d'un triangle :
 Une fois qu'on a les 3 points du triangle, l'afficher a l'écran est un probleme 2D : il suffit de dessiner une succession de lignes horizontales qui vont du haut du triangle jusque vers le bas. Les bords de ces lignes sont les bords du triangle, déterminées simplement par un algorithme de Brensenham (algorithme rapide pour tracer des lignes, sans calcul flottant, et facile à cabler) entre 2 sommets. (une arete étant une ligne)
Note : le fait que la distance de la caméra a chaque sommet aie été gardée permet de calculer tres rapidement, par interpolation, la distance d'un point quelconque du triangle a la camera.
Une fois qu'on a les 3 points du triangle, l'afficher a l'écran est un probleme 2D : il suffit de dessiner une succession de lignes horizontales qui vont du haut du triangle jusque vers le bas. Les bords de ces lignes sont les bords du triangle, déterminées simplement par un algorithme de Brensenham (algorithme rapide pour tracer des lignes, sans calcul flottant, et facile à cabler) entre 2 sommets. (une arete étant une ligne)
Note : le fait que la distance de la caméra a chaque sommet aie été gardée permet de calculer tres rapidement, par interpolation, la distance d'un point quelconque du triangle a la camera.
Z-buffer :
 Imaginons maintenant qu'il y aie plusieurs triangles dans la scene : l'un est devant l'autre : il va falloir ne pas afficher celui qui est derriere ! ou alors juste en partie !
Le probleme grandit également si les triangles s'entrecoupent : il y aura une partie de l'un qui cachera l'autre pour les 2 triangles...
Il n'est donc pas question que ce soit a l'utilisateur du moteur 3D de trier ses triangles : il faut que, meme si l'utilisateur envoie ses triangles dans le désordre, le monde s'affiche correctement, avec les parties cachées...
Comment faire pour gérer les faces cachées ? Et rapidement ?
On défini ce qu'on appelle un Z-buffer, c'est a dire un tableau, de la taille de la résolution choisie (ex : 1024*768), mais qui contiendra, non pas une couleur, mais un nombre.
Imaginons maintenant qu'il y aie plusieurs triangles dans la scene : l'un est devant l'autre : il va falloir ne pas afficher celui qui est derriere ! ou alors juste en partie !
Le probleme grandit également si les triangles s'entrecoupent : il y aura une partie de l'un qui cachera l'autre pour les 2 triangles...
Il n'est donc pas question que ce soit a l'utilisateur du moteur 3D de trier ses triangles : il faut que, meme si l'utilisateur envoie ses triangles dans le désordre, le monde s'affiche correctement, avec les parties cachées...
Comment faire pour gérer les faces cachées ? Et rapidement ?
On défini ce qu'on appelle un Z-buffer, c'est a dire un tableau, de la taille de la résolution choisie (ex : 1024*768), mais qui contiendra, non pas une couleur, mais un nombre.
Ce nombre sera la distance visible en un point x,y.
Au départ, les nombres sont grands : pour que tout soit visible.
Lorsque vous allez mettre un triangle, l'ordi va faire la méthode "Affichage rapide d'un triangle", mais avec un test en plus : sachant qu'il peut connaitre la distance en tout point du triangle a la caméra, pour chaque point x,y "pret a dessiner", il test si cette distance est inférieure au nombre x,y du Z-buffer. Si c'est le cas, alors le nouveau point est "devant" et on le dessine, sinon, alors le nouveau point est derriere, et on l'ignore.
Cette méthode entiere (englobant la rasterisation, jusqu'au Z-buffer), est faisable qu'avec des opérations simples, donc elle est CABLEE sur TOUTES les cartes graphiques actuelles, c'est a dire que l'algorithme est électronique, et donc des centaines de fois plus rapide que s'il ne l'était pas.
Cet algo de faces cachées consomme de la mémoire (le Z-buffer), mais il est rapide, et c'est celui choisi dans toutes les cartes graphiques.
(il existe d'autres algos, qui ne sont plus utilisés dans les jeux actuels : le scanlines, l'algo de Warnock, l'algo de Fuchs, ...)
Fonctions OpenGL :glEnable(GL_DEPTH_TEST); ...
Lumieres :
 Pour le moment, nous avons vu comment rendre de façon non réaliste : c'est a dire que si une face est rouge, on la dessine du meme rouge peut importe l'endroit ou elle se trouve.
Dans la réalité on va bien plus loin :
Pour le moment, nous avons vu comment rendre de façon non réaliste : c'est a dire que si une face est rouge, on la dessine du meme rouge peut importe l'endroit ou elle se trouve.
Dans la réalité on va bien plus loin :
On définit des lumieres : comme étant un point dans l'espace, associée d'une couleur de lumiere (lumiere blanche, lumiere rouge, etc... qui se propage dans toutes les directions de la meme façon a partir du point central de la lumiere.
(on peut définir d'autres types de lumieres, mais pour les jeux vidéos, on considere souvent uniquement ce genre de lumieres, dit "Spotlight")
Ainsi une face pourra etre a la lumiere, ou a l'ombre... Si une face est rouge, alors elle pourra etre plus ou moins foncée...
Le chapitre suivant introduit une notion fondamentale pour calculer la couleur exacte de la face en fonction de, ou des lumieres.
Fonctions OpenGL :glLight(...); ...
Normales :
 Les normales sont des notions fondamentales pour la lumiere, et bien d'autres choses.
Une normale est un vecteur, dont la longueur est 1 (on parle de vecteur normalisé)
Pour chaque face, donc chaque triangle, on défini une normale. C'est un vecteur orthognal au plan. Vous allez dire "il y a 2 vecteur orthogonaux a un plan : qui qui part dans un sens, l'autre dans l'autre sens.
Afin d'enelever l'ambiguité, tous les triangles passés sont ORIENTES dans le sens trigonométrique : c'est a dire que pour un triangle ABC, si A,B,C tourne dans le sens trigo (inverse des aiguilles d'une montre), alors la normale vient vers nous. La normale se calcule avec un produit vectoriel : AB^AC (noté aussi ABXAC)
Les normales sont des notions fondamentales pour la lumiere, et bien d'autres choses.
Une normale est un vecteur, dont la longueur est 1 (on parle de vecteur normalisé)
Pour chaque face, donc chaque triangle, on défini une normale. C'est un vecteur orthognal au plan. Vous allez dire "il y a 2 vecteur orthogonaux a un plan : qui qui part dans un sens, l'autre dans l'autre sens.
Afin d'enelever l'ambiguité, tous les triangles passés sont ORIENTES dans le sens trigonométrique : c'est a dire que pour un triangle ABC, si A,B,C tourne dans le sens trigo (inverse des aiguilles d'une montre), alors la normale vient vers nous. La normale se calcule avec un produit vectoriel : AB^AC (noté aussi ABXAC)
Bref, tout ça pour dire que l'on défini pour chaque triangle ou il "regarde"
Fonctions OpenGL :glNormal3f(...); ...
flat shading :
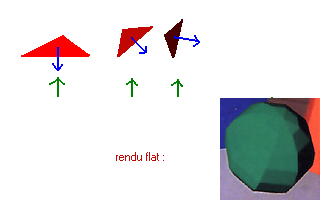 Nous arrivons a un type de rendu connu, qui gere les lumieres, il s'agit du Flat Shading.
Pour définir la couleur d'un triangle, on considere la normale a sa face N, puis on considere le vecteur E, qui sera le vecteur allant du centre du triangle G au centre de la lumiere L. (E = LG dans ma notation). On normalise les 2 vecteurs, c'est a dire qu'on réduit ou augmente leur taille pour que leur longueur fasse 1.
Nous arrivons a un type de rendu connu, qui gere les lumieres, il s'agit du Flat Shading.
Pour définir la couleur d'un triangle, on considere la normale a sa face N, puis on considere le vecteur E, qui sera le vecteur allant du centre du triangle G au centre de la lumiere L. (E = LG dans ma notation). On normalise les 2 vecteurs, c'est a dire qu'on réduit ou augmente leur taille pour que leur longueur fasse 1.
La magie opere ici : on calcule le produit scalaire N.E : si le triangle est bien en face, alors ce produit vaut 1, si le triangle est perpendiculaire, alors il vaut 0 : si la face ne regarde pas du tout la lumiere, alors il est négatif. Et selon l'orientation, on a toutes les valeurs possibles entre -1 et 1.
Ce nombre sera le coefficient d'ombrage : on va multiplier les composantes de la couleur du triangle par ce nombre : si on est bien en face, alors 1, donc on touche pas la couleur, si on est de travers, alors 0,5 par exemple, alors la couleur est + foncée, etc...
Si c'est négatif, alors 2 possibilités :
- on met 0 : alors le triangle est noir
- on prend la valeur absolue : alors les 2 faces du triangles sont identiques, et un triangle de "dos" sera comme s'il était de "face"
Le Flat shading est ce type de rendu la, qui gere déja la lumiere.
Fonctions OpenGL :glShadeModel(GL_FLAT);
Gouraud shading :
 Ce rendu est beau mais a un probleme : on voit NETTEMENT les triangles. En effet, chaque triangle est unicolor, donc ça fait des cassures avec ceux d'a coté : l'oeil y est sensible.
Pour palier ce probleme, un génie français grenoblois, Monsieur Gouraud, a eu une idée, qui est utilisée dans TOUS les jeux actuels, et cablé dans TOUTES les cartes graphiques actuelles, gérée par TOUS les moteurs 3D actuels : les différences de rendus sont étonnantes.
Ce rendu est beau mais a un probleme : on voit NETTEMENT les triangles. En effet, chaque triangle est unicolor, donc ça fait des cassures avec ceux d'a coté : l'oeil y est sensible.
Pour palier ce probleme, un génie français grenoblois, Monsieur Gouraud, a eu une idée, qui est utilisée dans TOUS les jeux actuels, et cablé dans TOUTES les cartes graphiques actuelles, gérée par TOUS les moteurs 3D actuels : les différences de rendus sont étonnantes.
Le principe est simple : au lieu de calculer une normale par face, on va calculer une normale par sommet. La normale pour un sommet donné se calcule comme un vecteur moyenne des faces adjascentes.
Pour chaque sommet, on a donc le produit scalaire N.E, et, au lieu d'assigner le meme coefficient d'ombrage a tout point du triangle, on va interpoler ce coefficient, de façon a faire un dégradé.
Comme il n'y a qu'une normale par sommet, pour plusieurs triangles adjascents, cela assure la continuité de couleur, et on n'a plus cette cassure de couleur due au Flat Shading.
Fonctions OpenGL :glShadeModel(GL_SMOOTH);
Phong shading :
 Voici un autre rendu plus joli que celui de Gouraud (un peu plus joli). Il se base sur le meme principe, sauf qu'au lieu d'interpoler les couleur des sommets, il interpole directement les normales aux sommets : il calcule donc la normale pour chaque point.
Probleme : interpoler des normales demande de calculer des racines carrées, et autant que de pixels : or les racines carrées ne se cablent pas pour le moment : impossible de faire de l'accélération matérielle pour. Donc Phong n'est pas utilisé dans les jeux : Gouraud reste le leader a ce jour.
Voici un autre rendu plus joli que celui de Gouraud (un peu plus joli). Il se base sur le meme principe, sauf qu'au lieu d'interpoler les couleur des sommets, il interpole directement les normales aux sommets : il calcule donc la normale pour chaque point.
Probleme : interpoler des normales demande de calculer des racines carrées, et autant que de pixels : or les racines carrées ne se cablent pas pour le moment : impossible de faire de l'accélération matérielle pour. Donc Phong n'est pas utilisé dans les jeux : Gouraud reste le leader a ce jour.
Un petit lien pour bien voir les différences entre flat/gouraud/phong :
http://www.cc.gatech.edu/classes/AY2004/cs4451a_fall/smodels/linint.html
et note : tous les triangles de la vache sont marron : si on n'utilise pas la lumiere, on a juste une silhouette marron de vache...
Antialisasing :
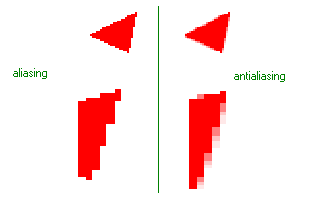 Passons maintenant a divers filtres.
Comme vous pouvez le voir, lorsque l'on trace une ligne oblique sur un ordi, on voit bien les pixels. Meme avec une bonne résolution, l'oeil est tres sensible a ces petite cassures. Ce n'est pas tres beau. Lors des rendus des triangles, on peut donc appliquer ce qu'on appelle l'antialiasing : il s'agit de fondre la ligne avec le décor derriere : le dessin parle de lui meme...
Passons maintenant a divers filtres.
Comme vous pouvez le voir, lorsque l'on trace une ligne oblique sur un ordi, on voit bien les pixels. Meme avec une bonne résolution, l'oeil est tres sensible a ces petite cassures. Ce n'est pas tres beau. Lors des rendus des triangles, on peut donc appliquer ce qu'on appelle l'antialiasing : il s'agit de fondre la ligne avec le décor derriere : le dessin parle de lui meme...
Textures :
 Voici maintenant une notion tres importante d'un moteur 3D : qui lui donne bien plus de puissance.
Jusqu'a présent, nous avons considéré des triangles unicolors (meme si on applique Gouraud derriere, a la base, c'est toujours unicolore)
Le principe des textures consiste a "tapisser" les triangles, et les quads (2 triangles assemblés) On les tapisse avec une image bitmap betement dessinée sous Paint.
Le moteur 3D va prendre l'image et la tordre pour l'inscrire correctement dans le Quad.
Voici maintenant une notion tres importante d'un moteur 3D : qui lui donne bien plus de puissance.
Jusqu'a présent, nous avons considéré des triangles unicolors (meme si on applique Gouraud derriere, a la base, c'est toujours unicolore)
Le principe des textures consiste a "tapisser" les triangles, et les quads (2 triangles assemblés) On les tapisse avec une image bitmap betement dessinée sous Paint.
Le moteur 3D va prendre l'image et la tordre pour l'inscrire correctement dans le Quad.
Fonctions OpenGL :glTeximage2d(...); glTexCoord2f(...); glBindtexture(...)
Texture Bluring :
 Imaginez que vous ayez dessiné une petite image, et que vous vouliez l'inscrire dans un grand Quad : vous allez voir de gros carrés.
Pour palier ce probleme, on peut faire du Texture Bluring, c'est a dire faire fondre les pixels les uns sur les autres pour créer un petit effet de flou, dont le but est d'empecher l'effet de pixelisation.
Imaginez que vous ayez dessiné une petite image, et que vous vouliez l'inscrire dans un grand Quad : vous allez voir de gros carrés.
Pour palier ce probleme, on peut faire du Texture Bluring, c'est a dire faire fondre les pixels les uns sur les autres pour créer un petit effet de flou, dont le but est d'empecher l'effet de pixelisation.
Ci contre : a gauche sans flou, a droite avec flou : cela prend intéret quand on est tres pret de la texture : partie zoomée en bas.
Mipmapping :
 Si vous faites avancer et reculer un Quad texturé, la machine va vous le rasteriser comme elle peut. Si le quad rasterisé est loin de sa taille d'origine, alors il se peut que ça fasse "moche". pour palier ce probleme, il faut préalablement dupliquer la texture en plusieurs petites 2 fois, 4 fois, 8 fois (des puissance de 2) plus petites. La machine va ensuite choisir la texture la mieux adaptée parmi ce mipmapping. Le résultat est visuel, les animations sont plus jolies, meme si ça coute + en mémoire. (VRAM de préférence). L'image n'est pas parlante, une animation l'est beaucoup plus.
Si vous faites avancer et reculer un Quad texturé, la machine va vous le rasteriser comme elle peut. Si le quad rasterisé est loin de sa taille d'origine, alors il se peut que ça fasse "moche". pour palier ce probleme, il faut préalablement dupliquer la texture en plusieurs petites 2 fois, 4 fois, 8 fois (des puissance de 2) plus petites. La machine va ensuite choisir la texture la mieux adaptée parmi ce mipmapping. Le résultat est visuel, les animations sont plus jolies, meme si ça coute + en mémoire. (VRAM de préférence). L'image n'est pas parlante, une animation l'est beaucoup plus.
Fonctions OpenGL :gluBuild2DMipmap(...);
Combiner le tout :
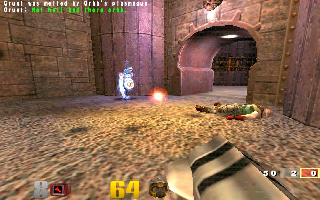 Si vous rendez des triangles ou quads blancs, avec des textures dessus, alors les texture apparaitront tel quel. Si vous rendez des quads rouges, alors la texture apparaitra comme si vous aviez mis un filtre rouge devant. Mais ce qui est intéressant est si vous rendez les quads blancs, avec Gouraud : dans ce cas, vous aurez un objet de base noir, blanc, avec des dégradés de gris. Combinez cela avec des textures, et vous avez des textures avec un dégradé de sombre, donc votre texture est éclairée de façon réaliste...
Si vous rendez des triangles ou quads blancs, avec des textures dessus, alors les texture apparaitront tel quel. Si vous rendez des quads rouges, alors la texture apparaitra comme si vous aviez mis un filtre rouge devant. Mais ce qui est intéressant est si vous rendez les quads blancs, avec Gouraud : dans ce cas, vous aurez un objet de base noir, blanc, avec des dégradés de gris. Combinez cela avec des textures, et vous avez des textures avec un dégradé de sombre, donc votre texture est éclairée de façon réaliste...
Et ce ne sont QUE des triangles texturés !! Rien d'autre !!
Effet brouillard :
 Parlons d'autre chose maintenant : on a vu le frustrum : il y a un plan "far" qui fait qu'au dela, plus rien n'est dessiné. Si vous laissez cela comme ça, alors on verra apparaitre les triangles au loin violemment : ce n'est pas réaliste...
Parlons d'autre chose maintenant : on a vu le frustrum : il y a un plan "far" qui fait qu'au dela, plus rien n'est dessiné. Si vous laissez cela comme ça, alors on verra apparaitre les triangles au loin violemment : ce n'est pas réaliste...
2 solutions :
- mettre le plan far plus loin --> meme les machines puissantes vont suffoquer...
- mettre du brouillard : pour cela la chose est simple : vou définissez une couleur de fond, par exemple du gris (car au loin dans le brouillard, tout est gris), puis l'astuce consiste a définir un seuil de profondeur a partir duquel le pixel devient de plus en plus gris, ainsi, vous arrivez progressivement au gris total, sans démarquation.
Fonctions OpenGL :glEnable(GL_FOG);
Retour
 Un écran est un repere 2D. Le repere est orienté comme sur le schéma.
Ainsi, chaque pixel est représenté par une coordonnée x,y. La
résolution de votre écran (ou de votre fenetre) défini le nombre de
pixels. Par exemple 1024*768 pixels, etc...
x varie dans ce cas entre 0 et 1023, y entre 0 et 767. Le point en
bas a droite aura pour coordonnée 1023,767.
Un ensemble rectangulaire de pixels est appelé un bitmap.
Ainsi l'écran est un bitmap.
Un écran est un repere 2D. Le repere est orienté comme sur le schéma.
Ainsi, chaque pixel est représenté par une coordonnée x,y. La
résolution de votre écran (ou de votre fenetre) défini le nombre de
pixels. Par exemple 1024*768 pixels, etc...
x varie dans ce cas entre 0 et 1023, y entre 0 et 767. Le point en
bas a droite aura pour coordonnée 1023,767.
Un ensemble rectangulaire de pixels est appelé un bitmap.
Ainsi l'écran est un bitmap.
 Toute couleur sur ordi est définie par 3 composantes : rouge, vert,
bleu. En dosant les intensités de ces 3 couleurs, on reforme TOUTES
les couleurs. Par exemple : le noir est 0% de rouge, 0% de vert, 0%
de bleu. Le blanc, c'est 100% des 3. Le violet, c'est 100% de rouge,
100% de bleu, 0% de vert...
Toute couleur sur ordi est définie par 3 composantes : rouge, vert,
bleu. En dosant les intensités de ces 3 couleurs, on reforme TOUTES
les couleurs. Par exemple : le noir est 0% de rouge, 0% de vert, 0%
de bleu. Le blanc, c'est 100% des 3. Le violet, c'est 100% de rouge,
100% de bleu, 0% de vert...
 A chaque pixel est associé une couleur. C'est uniquement ainsi qu'on
défini une image.
Il existe plusieurs formats pour coder une couleur.
- mode indexé 16 couleurs (a) : chaque pixel coute 4 bits (1/2
octet). 1/2 octet stocke 16 possibilités, donc dans cette résolution,
on ne pourra avoir que 16 couleur affichables. On défini pour chaque
pixel du bitmap un nombre entre 0 et 15. Ailleurs en mémoire, il
existe ce qu'on appelle une palette. C'est cette palette qui dit "la
couleur 0 est du noir, la couleur 1 est du blanc, la couleur 2 est du
bleu, etc...". L'avantage de cette méthode est que si on change la
palette (on dit que le 2 est maintenant du rouge), alors tous les
pixels bleus de l'écran deviennent automatiquement rouge.
A chaque pixel est associé une couleur. C'est uniquement ainsi qu'on
défini une image.
Il existe plusieurs formats pour coder une couleur.
- mode indexé 16 couleurs (a) : chaque pixel coute 4 bits (1/2
octet). 1/2 octet stocke 16 possibilités, donc dans cette résolution,
on ne pourra avoir que 16 couleur affichables. On défini pour chaque
pixel du bitmap un nombre entre 0 et 15. Ailleurs en mémoire, il
existe ce qu'on appelle une palette. C'est cette palette qui dit "la
couleur 0 est du noir, la couleur 1 est du blanc, la couleur 2 est du
bleu, etc...". L'avantage de cette méthode est que si on change la
palette (on dit que le 2 est maintenant du rouge), alors tous les
pixels bleus de l'écran deviennent automatiquement rouge. Toute la 2D repose sur le blitting. L'écran est un bitmap. On colle
par exemple un bitmap de la taille de l'écran dessus, qui fera le
fond, puis on charge d'autres petits bitmaps rectangulaires, et on
coupe et colle les images sur le bitmap de l'écran, du collage en
somme !
On appelle cette opération "blit".
Cependant, si on s'arrete la, alors on voit nettement que l'on colle
des rectangles (a).
On défini une "keycolor", c'est a dire une couleur qui sera invisible
pour chaque bitmap. Ainsi, lorsqu'un bitmap est collé, la couleur
invisible n'apparait pas, ce qui rend la chose plus réaliste (b)
Toute la 2D repose sur le blitting. L'écran est un bitmap. On colle
par exemple un bitmap de la taille de l'écran dessus, qui fera le
fond, puis on charge d'autres petits bitmaps rectangulaires, et on
coupe et colle les images sur le bitmap de l'écran, du collage en
somme !
On appelle cette opération "blit".
Cependant, si on s'arrete la, alors on voit nettement que l'on colle
des rectangles (a).
On défini une "keycolor", c'est a dire une couleur qui sera invisible
pour chaque bitmap. Ainsi, lorsqu'un bitmap est collé, la couleur
invisible n'apparait pas, ce qui rend la chose plus réaliste (b) Nous voulons faire une animation. Pour cela, il faut, pour chaque
image, coller le personnage un peu plus loin que l'image d'avant.
Pour cela, il faut d'abord effacer l'image actuelle, puis la recréer
en mettant le perso plus loin. L'ordinateur a beau etre rapide
(plusieurs milliers voir centaines de milliers de blit par seconde),
si on fait cela, on verra notre personnage clignoter : car pendant
une fraction de seconde, entre le temps ou c'est effacé, et le temps
ou le personnage est redessiné plus loin, il n'y a plus le personnage
: donc il apparait et disparait tres vite --> clignotement.
Pour palier ce probleme, on défini 2 bitmap d'écrans. L'un est
visible a l'écran. Pendant ce temps, on prépare, sur le 2e, invisible
a l'écran, la nouvelle image. Une fois fini, on "flip", c'est a dire
qu'on dit que maintenant, c'est la 2e image qui est affichée, et la
1ere image que l'on va pouvoir modifier. La 2e image, toute prete
remplace la 1ere : comme au cinéma, on n'a plus de clignotement.
A la différence du cinéma qui stocke toutes ses images, ici, l'ordi
calcule sans arret l'image suivante, et l'affiche qu'une fois
terminée, afin de calculer la suivante de nouveau...
Nous voulons faire une animation. Pour cela, il faut, pour chaque
image, coller le personnage un peu plus loin que l'image d'avant.
Pour cela, il faut d'abord effacer l'image actuelle, puis la recréer
en mettant le perso plus loin. L'ordinateur a beau etre rapide
(plusieurs milliers voir centaines de milliers de blit par seconde),
si on fait cela, on verra notre personnage clignoter : car pendant
une fraction de seconde, entre le temps ou c'est effacé, et le temps
ou le personnage est redessiné plus loin, il n'y a plus le personnage
: donc il apparait et disparait tres vite --> clignotement.
Pour palier ce probleme, on défini 2 bitmap d'écrans. L'un est
visible a l'écran. Pendant ce temps, on prépare, sur le 2e, invisible
a l'écran, la nouvelle image. Une fois fini, on "flip", c'est a dire
qu'on dit que maintenant, c'est la 2e image qui est affichée, et la
1ere image que l'on va pouvoir modifier. La 2e image, toute prete
remplace la 1ere : comme au cinéma, on n'a plus de clignotement.
A la différence du cinéma qui stocke toutes ses images, ici, l'ordi
calcule sans arret l'image suivante, et l'affiche qu'une fois
terminée, afin de calculer la suivante de nouveau... lorsqu'un personnage est sur le bord de l'écran, il faut qu'on ne le
voie qu'a moitié. Pour cela, il ne faut donc pas l'afficher
completement, mais juste la partie visible, il faut donc une phase de
prédécoupage, ou l'ordi selectionne juste la partie a afficher. C'est
un "clipping". Tous les moteurs actuels gerent le clipping
automatiquement : si vous blittez en personnage sur l'écran, sur le
bord, ou meme dehors, ils gerent ça tout seul. Les cartes graphiques
sont meme en partie faites pour cela.
lorsqu'un personnage est sur le bord de l'écran, il faut qu'on ne le
voie qu'a moitié. Pour cela, il ne faut donc pas l'afficher
completement, mais juste la partie visible, il faut donc une phase de
prédécoupage, ou l'ordi selectionne juste la partie a afficher. C'est
un "clipping". Tous les moteurs actuels gerent le clipping
automatiquement : si vous blittez en personnage sur l'écran, sur le
bord, ou meme dehors, ils gerent ça tout seul. Les cartes graphiques
sont meme en partie faites pour cela.
 L'ordinateur contient plusieurs mémoires : une centrale, appelée RAM,
et une sur la carte graphique, appelée VRAM. Si on garde toutes les
images en RAM, alors, a chaque nouvelle frame (nouvelle image
calculée), (donc 50 par secondes par exemple si on veut une animation
fluide), toute l'image est evoyée sur le bus. A titre indicatif, une
image de 1024*768, 32bits, fait a peu pres 4Mo. Si on doit en envoyer
50 par seconde, cela fait une taux de circulation de 50*4 = 200 Mo
sur le bus, rien que pour la vidéo. C'est énorme : beaucoup d'ordis
rament. Je précise que certains joueurs trouvent que 50 images par secondes,
c'est lent, et veulent avoisiner les 100 fps (frame per second = images par secondes)
L'ordinateur contient plusieurs mémoires : une centrale, appelée RAM,
et une sur la carte graphique, appelée VRAM. Si on garde toutes les
images en RAM, alors, a chaque nouvelle frame (nouvelle image
calculée), (donc 50 par secondes par exemple si on veut une animation
fluide), toute l'image est evoyée sur le bus. A titre indicatif, une
image de 1024*768, 32bits, fait a peu pres 4Mo. Si on doit en envoyer
50 par seconde, cela fait une taux de circulation de 50*4 = 200 Mo
sur le bus, rien que pour la vidéo. C'est énorme : beaucoup d'ordis
rament. Je précise que certains joueurs trouvent que 50 images par secondes,
c'est lent, et veulent avoisiner les 100 fps (frame per second = images par secondes) Le repere 3D est un repere dans l'espace : l'origine est le point O, et la base est x,y,z.
Ainsi, dans l'espace, on représente un point par 3 coordonnées.
Le repere 3D est un repere dans l'espace : l'origine est le point O, et la base est x,y,z.
Ainsi, dans l'espace, on représente un point par 3 coordonnées. Tous les moteurs 3D temps réels actuels marchent de façon simple : vous donnez des triangles a la carte graphique, et elle les affiche correctement. Un triangle, c'est 3 points, et 3 points, c'est 3 nombres a virgule, donc ça fait 9 nombres a passer par triangle. Nous verrons comment cela marche par la suite.
Tous les moteurs 3D temps réels actuels marchent de façon simple : vous donnez des triangles a la carte graphique, et elle les affiche correctement. Un triangle, c'est 3 points, et 3 points, c'est 3 nombres a virgule, donc ça fait 9 nombres a passer par triangle. Nous verrons comment cela marche par la suite. Pour modéliser une scene en 3D, il faut donc donner des triangles dans l'espace. Cependant, il faut également définir une caméra, pour savoir de quel endroit on regarde la scene.
La caméra se défini, par 3 données, disons que la caméra est vos yeux :
Pour modéliser une scene en 3D, il faut donc donner des triangles dans l'espace. Cependant, il faut également définir une caméra, pour savoir de quel endroit on regarde la scene.
La caméra se défini, par 3 données, disons que la caméra est vos yeux : Vous le savez peut etre, mais il existe des caméras grand angle, et des caméras de moins grand angle. Les moteurs 3D permettent de paramétrer toute sorte de parametres, qui définiront le frustrum de vision, c'est a dire que ce que vous verrez est ce qu'il y aura a l'intérieur de cette pyramide coupée verte, et vous ne verrez pas ce qu'il y a à l'extérieur.
On définit le frustrum de la manière suivante (il en existe d'autres manieres mais ça revient au meme)
Vous le savez peut etre, mais il existe des caméras grand angle, et des caméras de moins grand angle. Les moteurs 3D permettent de paramétrer toute sorte de parametres, qui définiront le frustrum de vision, c'est a dire que ce que vous verrez est ce qu'il y aura a l'intérieur de cette pyramide coupée verte, et vous ne verrez pas ce qu'il y a à l'extérieur.
On définit le frustrum de la manière suivante (il en existe d'autres manieres mais ça revient au meme) Ce monde en 3D composé de nombres réels, qui se trouve en mémoire, composé de cette soupe de triangles, doit, pour etre rendu, etre projeté sur l'écran 2D (ce sera un dessin 3D sur l'écran). Pour cela, l'ordi garde en mémoire un tableau de 1024*768 pixels par exemple, avec une certaine profondeur de couleur (voir théorie 2D la dessus) Tout comme la 2D, il sera souhaitable de gérer un double buffering, donc avoir 2 tableaux de couleurs que l'on "flip"
La différence, c'est que les images ne seront pas faites a partir de copier coller de vignettes comme dans la 2D, mais d'un monde 3D rasterisé, c'est a dire projeté sur l'écran.
Pour rasteriser, l'ordi effectue l'opération suivante :
pour chaque triangle, il calcule les coordonnée des 3 sommets projetés (voir ce calcul plus loin), en s'appuyant sur les parametres définis de la caméra et de la position des triangles dans l'espace.
Il conserve en outre la distance de chaque sommet a la caméra. Pour que ce soit rapide, il considere la distance au carré, ce qui évite un calcul de racine carrée.
Sachant que la projection d'un triangle est un triangle, il lui suffit de dessiner le triangle a l'écran...
si les projections des sommets sont a l'extérieur de l'écran, il ne rend pas les triangles, ou alors il les clip. (voir clipping dans la 2D)
Ce monde en 3D composé de nombres réels, qui se trouve en mémoire, composé de cette soupe de triangles, doit, pour etre rendu, etre projeté sur l'écran 2D (ce sera un dessin 3D sur l'écran). Pour cela, l'ordi garde en mémoire un tableau de 1024*768 pixels par exemple, avec une certaine profondeur de couleur (voir théorie 2D la dessus) Tout comme la 2D, il sera souhaitable de gérer un double buffering, donc avoir 2 tableaux de couleurs que l'on "flip"
La différence, c'est que les images ne seront pas faites a partir de copier coller de vignettes comme dans la 2D, mais d'un monde 3D rasterisé, c'est a dire projeté sur l'écran.
Pour rasteriser, l'ordi effectue l'opération suivante :
pour chaque triangle, il calcule les coordonnée des 3 sommets projetés (voir ce calcul plus loin), en s'appuyant sur les parametres définis de la caméra et de la position des triangles dans l'espace.
Il conserve en outre la distance de chaque sommet a la caméra. Pour que ce soit rapide, il considere la distance au carré, ce qui évite un calcul de racine carrée.
Sachant que la projection d'un triangle est un triangle, il lui suffit de dessiner le triangle a l'écran...
si les projections des sommets sont a l'extérieur de l'écran, il ne rend pas les triangles, ou alors il les clip. (voir clipping dans la 2D)
 Une fois qu'on a les 3 points du triangle, l'afficher a l'écran est un probleme 2D : il suffit de dessiner une succession de lignes horizontales qui vont du haut du triangle jusque vers le bas. Les bords de ces lignes sont les bords du triangle, déterminées simplement par un algorithme de Brensenham (algorithme rapide pour tracer des lignes, sans calcul flottant, et facile à cabler) entre 2 sommets. (une arete étant une ligne)
Note : le fait que la distance de la caméra a chaque sommet aie été gardée permet de calculer tres rapidement, par interpolation, la distance d'un point quelconque du triangle a la camera.
Une fois qu'on a les 3 points du triangle, l'afficher a l'écran est un probleme 2D : il suffit de dessiner une succession de lignes horizontales qui vont du haut du triangle jusque vers le bas. Les bords de ces lignes sont les bords du triangle, déterminées simplement par un algorithme de Brensenham (algorithme rapide pour tracer des lignes, sans calcul flottant, et facile à cabler) entre 2 sommets. (une arete étant une ligne)
Note : le fait que la distance de la caméra a chaque sommet aie été gardée permet de calculer tres rapidement, par interpolation, la distance d'un point quelconque du triangle a la camera.
 Imaginons maintenant qu'il y aie plusieurs triangles dans la scene : l'un est devant l'autre : il va falloir ne pas afficher celui qui est derriere ! ou alors juste en partie !
Le probleme grandit également si les triangles s'entrecoupent : il y aura une partie de l'un qui cachera l'autre pour les 2 triangles...
Il n'est donc pas question que ce soit a l'utilisateur du moteur 3D de trier ses triangles : il faut que, meme si l'utilisateur envoie ses triangles dans le désordre, le monde s'affiche correctement, avec les parties cachées...
Comment faire pour gérer les faces cachées ? Et rapidement ?
On défini ce qu'on appelle un Z-buffer, c'est a dire un tableau, de la taille de la résolution choisie (ex : 1024*768), mais qui contiendra, non pas une couleur, mais un nombre.
Imaginons maintenant qu'il y aie plusieurs triangles dans la scene : l'un est devant l'autre : il va falloir ne pas afficher celui qui est derriere ! ou alors juste en partie !
Le probleme grandit également si les triangles s'entrecoupent : il y aura une partie de l'un qui cachera l'autre pour les 2 triangles...
Il n'est donc pas question que ce soit a l'utilisateur du moteur 3D de trier ses triangles : il faut que, meme si l'utilisateur envoie ses triangles dans le désordre, le monde s'affiche correctement, avec les parties cachées...
Comment faire pour gérer les faces cachées ? Et rapidement ?
On défini ce qu'on appelle un Z-buffer, c'est a dire un tableau, de la taille de la résolution choisie (ex : 1024*768), mais qui contiendra, non pas une couleur, mais un nombre. Pour le moment, nous avons vu comment rendre de façon non réaliste : c'est a dire que si une face est rouge, on la dessine du meme rouge peut importe l'endroit ou elle se trouve.
Dans la réalité on va bien plus loin :
Pour le moment, nous avons vu comment rendre de façon non réaliste : c'est a dire que si une face est rouge, on la dessine du meme rouge peut importe l'endroit ou elle se trouve.
Dans la réalité on va bien plus loin : Les normales sont des notions fondamentales pour la lumiere, et bien d'autres choses.
Une normale est un vecteur, dont la longueur est 1 (on parle de vecteur normalisé)
Pour chaque face, donc chaque triangle, on défini une normale. C'est un vecteur orthognal au plan. Vous allez dire "il y a 2 vecteur orthogonaux a un plan : qui qui part dans un sens, l'autre dans l'autre sens.
Afin d'enelever l'ambiguité, tous les triangles passés sont ORIENTES dans le sens trigonométrique : c'est a dire que pour un triangle ABC, si A,B,C tourne dans le sens trigo (inverse des aiguilles d'une montre), alors la normale vient vers nous. La normale se calcule avec un produit vectoriel : AB^AC (noté aussi ABXAC)
Les normales sont des notions fondamentales pour la lumiere, et bien d'autres choses.
Une normale est un vecteur, dont la longueur est 1 (on parle de vecteur normalisé)
Pour chaque face, donc chaque triangle, on défini une normale. C'est un vecteur orthognal au plan. Vous allez dire "il y a 2 vecteur orthogonaux a un plan : qui qui part dans un sens, l'autre dans l'autre sens.
Afin d'enelever l'ambiguité, tous les triangles passés sont ORIENTES dans le sens trigonométrique : c'est a dire que pour un triangle ABC, si A,B,C tourne dans le sens trigo (inverse des aiguilles d'une montre), alors la normale vient vers nous. La normale se calcule avec un produit vectoriel : AB^AC (noté aussi ABXAC) Nous arrivons a un type de rendu connu, qui gere les lumieres, il s'agit du Flat Shading.
Pour définir la couleur d'un triangle, on considere la normale a sa face N, puis on considere le vecteur E, qui sera le vecteur allant du centre du triangle G au centre de la lumiere L. (E = LG dans ma notation). On normalise les 2 vecteurs, c'est a dire qu'on réduit ou augmente leur taille pour que leur longueur fasse 1.
Nous arrivons a un type de rendu connu, qui gere les lumieres, il s'agit du Flat Shading.
Pour définir la couleur d'un triangle, on considere la normale a sa face N, puis on considere le vecteur E, qui sera le vecteur allant du centre du triangle G au centre de la lumiere L. (E = LG dans ma notation). On normalise les 2 vecteurs, c'est a dire qu'on réduit ou augmente leur taille pour que leur longueur fasse 1. Ce rendu est beau mais a un probleme : on voit NETTEMENT les triangles. En effet, chaque triangle est unicolor, donc ça fait des cassures avec ceux d'a coté : l'oeil y est sensible.
Pour palier ce probleme, un génie français grenoblois, Monsieur Gouraud, a eu une idée, qui est utilisée dans TOUS les jeux actuels, et cablé dans TOUTES les cartes graphiques actuelles, gérée par TOUS les moteurs 3D actuels : les différences de rendus sont étonnantes.
Ce rendu est beau mais a un probleme : on voit NETTEMENT les triangles. En effet, chaque triangle est unicolor, donc ça fait des cassures avec ceux d'a coté : l'oeil y est sensible.
Pour palier ce probleme, un génie français grenoblois, Monsieur Gouraud, a eu une idée, qui est utilisée dans TOUS les jeux actuels, et cablé dans TOUTES les cartes graphiques actuelles, gérée par TOUS les moteurs 3D actuels : les différences de rendus sont étonnantes. Voici un autre rendu plus joli que celui de Gouraud (un peu plus joli). Il se base sur le meme principe, sauf qu'au lieu d'interpoler les couleur des sommets, il interpole directement les normales aux sommets : il calcule donc la normale pour chaque point.
Probleme : interpoler des normales demande de calculer des racines carrées, et autant que de pixels : or les racines carrées ne se cablent pas pour le moment : impossible de faire de l'accélération matérielle pour. Donc Phong n'est pas utilisé dans les jeux : Gouraud reste le leader a ce jour.
Voici un autre rendu plus joli que celui de Gouraud (un peu plus joli). Il se base sur le meme principe, sauf qu'au lieu d'interpoler les couleur des sommets, il interpole directement les normales aux sommets : il calcule donc la normale pour chaque point.
Probleme : interpoler des normales demande de calculer des racines carrées, et autant que de pixels : or les racines carrées ne se cablent pas pour le moment : impossible de faire de l'accélération matérielle pour. Donc Phong n'est pas utilisé dans les jeux : Gouraud reste le leader a ce jour. Passons maintenant a divers filtres.
Comme vous pouvez le voir, lorsque l'on trace une ligne oblique sur un ordi, on voit bien les pixels. Meme avec une bonne résolution, l'oeil est tres sensible a ces petite cassures. Ce n'est pas tres beau. Lors des rendus des triangles, on peut donc appliquer ce qu'on appelle l'antialiasing : il s'agit de fondre la ligne avec le décor derriere : le dessin parle de lui meme...
Passons maintenant a divers filtres.
Comme vous pouvez le voir, lorsque l'on trace une ligne oblique sur un ordi, on voit bien les pixels. Meme avec une bonne résolution, l'oeil est tres sensible a ces petite cassures. Ce n'est pas tres beau. Lors des rendus des triangles, on peut donc appliquer ce qu'on appelle l'antialiasing : il s'agit de fondre la ligne avec le décor derriere : le dessin parle de lui meme...
 Voici maintenant une notion tres importante d'un moteur 3D : qui lui donne bien plus de puissance.
Jusqu'a présent, nous avons considéré des triangles unicolors (meme si on applique Gouraud derriere, a la base, c'est toujours unicolore)
Le principe des textures consiste a "tapisser" les triangles, et les quads (2 triangles assemblés) On les tapisse avec une image bitmap betement dessinée sous Paint.
Le moteur 3D va prendre l'image et la tordre pour l'inscrire correctement dans le Quad.
Voici maintenant une notion tres importante d'un moteur 3D : qui lui donne bien plus de puissance.
Jusqu'a présent, nous avons considéré des triangles unicolors (meme si on applique Gouraud derriere, a la base, c'est toujours unicolore)
Le principe des textures consiste a "tapisser" les triangles, et les quads (2 triangles assemblés) On les tapisse avec une image bitmap betement dessinée sous Paint.
Le moteur 3D va prendre l'image et la tordre pour l'inscrire correctement dans le Quad.
 Imaginez que vous ayez dessiné une petite image, et que vous vouliez l'inscrire dans un grand Quad : vous allez voir de gros carrés.
Pour palier ce probleme, on peut faire du Texture Bluring, c'est a dire faire fondre les pixels les uns sur les autres pour créer un petit effet de flou, dont le but est d'empecher l'effet de pixelisation.
Imaginez que vous ayez dessiné une petite image, et que vous vouliez l'inscrire dans un grand Quad : vous allez voir de gros carrés.
Pour palier ce probleme, on peut faire du Texture Bluring, c'est a dire faire fondre les pixels les uns sur les autres pour créer un petit effet de flou, dont le but est d'empecher l'effet de pixelisation. Si vous faites avancer et reculer un Quad texturé, la machine va vous le rasteriser comme elle peut. Si le quad rasterisé est loin de sa taille d'origine, alors il se peut que ça fasse "moche". pour palier ce probleme, il faut préalablement dupliquer la texture en plusieurs petites 2 fois, 4 fois, 8 fois (des puissance de 2) plus petites. La machine va ensuite choisir la texture la mieux adaptée parmi ce mipmapping. Le résultat est visuel, les animations sont plus jolies, meme si ça coute + en mémoire. (VRAM de préférence). L'image n'est pas parlante, une animation l'est beaucoup plus.
Si vous faites avancer et reculer un Quad texturé, la machine va vous le rasteriser comme elle peut. Si le quad rasterisé est loin de sa taille d'origine, alors il se peut que ça fasse "moche". pour palier ce probleme, il faut préalablement dupliquer la texture en plusieurs petites 2 fois, 4 fois, 8 fois (des puissance de 2) plus petites. La machine va ensuite choisir la texture la mieux adaptée parmi ce mipmapping. Le résultat est visuel, les animations sont plus jolies, meme si ça coute + en mémoire. (VRAM de préférence). L'image n'est pas parlante, une animation l'est beaucoup plus.
 Si vous rendez des triangles ou quads blancs, avec des textures dessus, alors les texture apparaitront tel quel. Si vous rendez des quads rouges, alors la texture apparaitra comme si vous aviez mis un filtre rouge devant. Mais ce qui est intéressant est si vous rendez les quads blancs, avec Gouraud : dans ce cas, vous aurez un objet de base noir, blanc, avec des dégradés de gris. Combinez cela avec des textures, et vous avez des textures avec un dégradé de sombre, donc votre texture est éclairée de façon réaliste...
Si vous rendez des triangles ou quads blancs, avec des textures dessus, alors les texture apparaitront tel quel. Si vous rendez des quads rouges, alors la texture apparaitra comme si vous aviez mis un filtre rouge devant. Mais ce qui est intéressant est si vous rendez les quads blancs, avec Gouraud : dans ce cas, vous aurez un objet de base noir, blanc, avec des dégradés de gris. Combinez cela avec des textures, et vous avez des textures avec un dégradé de sombre, donc votre texture est éclairée de façon réaliste... Parlons d'autre chose maintenant : on a vu le frustrum : il y a un plan "far" qui fait qu'au dela, plus rien n'est dessiné. Si vous laissez cela comme ça, alors on verra apparaitre les triangles au loin violemment : ce n'est pas réaliste...
Parlons d'autre chose maintenant : on a vu le frustrum : il y a un plan "far" qui fait qu'au dela, plus rien n'est dessiné. Si vous laissez cela comme ça, alors on verra apparaitre les triangles au loin violemment : ce n'est pas réaliste...